Mathematics & God
Why Many Vital Equations Are Beautiful
Clickable Table of Contents:
- See Einstein's lab where he discovered special relativity
- Einstein, et al., making discoveries with mind (not with the senses)
- Comprehending Einstein's incomprehensible gulf between matter and ideas
- The multiverse is a measurement tool like a yardstick used to measure...
- Astounding and unexpectedly beautiful equations like E = mc2
- The square root of negative one reveals the Creator's intellect
- For discerning morality mathematics is useless
- Did Richard Feynman see God?
- Mathematicians, evolutionists, and the Wistar report
- Is math science? About those who say no...
* How Einstein and Others Can Use their Minds to Make Discoveries: Materialists will claim that you can only learn what your five sense tell you, but then, which of their five senses told them that? As author James Nickel recently told RSR, mathematicians turn away from the physical universe and yet make astounding discoveries that help to explain the world of matter and energy. Using their minds, rather than microscopes or telescopes, theoreticians make discoveries years, decades, and even centuries before their empirical counterparts make the same discoveries by observational science. Some examples:
- Max Planck, in the year 1900, by thinking about how to solve a math problem in physics, discovered the Planck constant, the foundation of the quantum mechanics revolution of the 1920s.
- Paul Dirac, by thinking, discovered the positron (the electron's antimatter counterpart) in 1928, prior to physicists noticing it in 1929 and confirming its existence its 1932.
- Peter Higgs in 1964 saw in his mind the existence of the subatomic Higgs boson almost a half century before scientists empirically found it using the nine-billion dollar Large Hadron Collider.
- James Clerk Maxwell, father of the science of electromagnetic radiation, discovered in 1859 in one of the greatest applications of math to physics, and so, not with a telescope but by thought, that Saturn's rings were not, as had been supposed, solid, nor a continuous fluid, but were made up of disconnected particles, a discovery confirmed 122 years later with NASA's Voyager 2 mission.
- Maxwell also discovered, not by experiment but with his mind, that a moving electric field will create a magnetic field, and in 1862 again only with his mind and mathematics, discovered that light and electromagnetism are the same phenomenon with a calculation of the self-propagating speed of an EM radiation wave showing it to approximate the speed of light, for it is light, not empirically observed for another 20 years.
- Mathematician and astronomer Joseph-Louis Lagrange discovered gravitationally stable Lagrange Points. He was born in Turin, Italy in 1736 and discovered two of these points with his mind, a few years after Leonhard Euler first discovered three, with his mind! Today we position exploratory satellites at these points where also two major but temporary (transient) dust clouds are held in place.
- Time's Albert Einstein: The Enduring Legacy says that today's "high precision instruments such as atomic clocks and lasers... have shown that he was absolutely on target with the equations he worked out with nothing more than a pencil." And describing Einstein's visit with his wife in 1931 to see the 100-inch reflecting telescope at California's Mount Wilson Observatory, Richard Lacayo writes for Time magazine that, "When the astronomers there boasted that their telescope could probe the structure of the universe, Elsa quipped: 'My husband does that on the back of an old envelope.'"
* Einstein's Lab Where He Discovered Special Relativity: Many materialists claim that you can only know that which your five senses tell you. This is one of the ten atheist cliches which RSR refutes in eight seconds or less. But no atheist could ever learn from any of his five senses that he can only know what his five senses tell him. Likewise, Einstein's five senses didn't reveal relativity to him. So we watch as today's materialists are becoming increasingly uncomfortable with the non-physicality of information, with the reality of logic, with the existence of math and absolute morality, and even with the existence of truth itself. (See a list of non-physical things at rsr.org/physical.)
* Einstein Confuses Lawrence Krauss: As an extraordinary example of today's atheists trying to distance themselves from the realm of ideas, theoretical physicist Lawrence Krauss (emphasis on the theoretical), in his book A Universe from Nothing, attempts to refute the phenomenon described by Nickel, that mathematicians often use their minds, rather than scientific equipment, to make astounding discoveries of the physical universe. In support of his denial, he presents an anecdote about Albert Einstein which, even in Krauss' own telling, EXACTLY contradicts Krauss' own reason for telling the story. Einstein used telescopes, yes, to make an astronomical observation, yes, but NOT to form his theory, for his theory had already been written on paper. Discover magazine's Richard Panek explains:
In the late 17th century, Isaac Newton helped inaugurate a scientific revolution by taking Galileo's observations of the heavens' motions and expressing them mathematically. Then in the early 20th century, Albert Einstein helped inaugurate a second scientific revolution by reversing that process, taking his own calculations and looking for their physical expression in the heavens.
* Rather Touchy Atheists: Atheists are rather touchy on this subject. For example, when this RSR article was first posted, we provided Cherenkov radiation as an example of a pre-discovery as already described for years on Wikipedia. Yet shortly after we made that point (and the link), the Wikipedia article was edited (as happens, including for example when we posted about mammoths) to downplay the extraordinary significance of the prediction of this radiation made in the 1880s by Oliver Heaviside! But to take this further, this self-taught physicist also illustrated the main point of this article when he realized that complex numbers which include the imaginary square root of -1 were useful in describing electrical circuits! In the Krauss' example above, Einstein used his eyes to make an observation to confirm the theory he already established with his mind. For Einstein is not renowned for his eyesight but for his intellect.
* Comprehending the Gulf that Einstein said was Incomprehensible: Einstein wrote that it was "incomprehensible" that the non-physical realm of "ideas" could even exist in a physical world. It was incomprehensible to him that non-physical mathematics, which itself is not composed of matter or energy, could describe so beautifully the physical universe. After realizing that the physical laws do not address morality, Einstein then wondered even about the physical laws themselves and why it should be that mathematical ideas, which are non-physical, should correspond so well to the physical universe. In 1921 Einstein asked, "How can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality?"
* Einstein's Gulf: Even though Einstein was uncomfortable with this concept, fifteen years later he was still wrestling with the same unshakable observation. For in 1936 Einstein famously wrote that, "the eternal mystery of the world is its comprehensibility." Then in 1944, remarking about atheist Bertrand Russell, he described the ability to get from matter to ideas as a "gulf–logically unbridgeable," which some scientists and linguists refer to as Einstein's Gulf. For while matter can be arranged to represent data, information itself is not material. Richard Walker, in his value-added re-airing of today's RSR program on Boston's WROL radio, mentioned the iconic article with a title that reiterates Einstein's point, The Unreasonable Effectiveness of Mathematics in the Natural Sciences, by Nobel-prize winning physicist Eugene Wigner.)
However, introduce a Designer, and Wigner's observation flips into the reasonable effectiveness of mathematics! So the explanation for this phenomenon is one that Einstein (and Krauss) reject a priori. Mankind can understand the correspondence between pure ideas and physical phenomenon only by the realization that the universe was designed in the mind of God. So its workings can be discovered by the mind of men who are made in God's image. Brilliant though pagan Indian mathematician Srinivasa Ramanujan once said, "An equation for me has no meaning unless it expresses a thought of God." (Ramanujan's celebrated biographer Robert Kanigel wrote, "openness to supernatural influences... left him receptive to what those equipped with more purely logical gifts could not see." And of course logic enables men to perceive more than Kanigel assumes there.) Einstein however denied the existence of God so he was left to his confusion, whereas Kepler understood and is paraphrased, We are thinking God's thoughts after Him.
* The Multiverse Yardstick: In the years since Einstein observed the gulf, things have gotten so bad for materialists that they have introduced a new measurement tool called the multiverse. The multiverse is a yardstick used to measure the strength of the fine tuning argument for God's existence. It's speedy acceptance is measuring the desperation of the materialist. So the one-word proof that the big bang theory has failed in its purpose to provide an explanation for the existence of the universe: multiverse! Finally, if you Google: fine tuning, RSR's page is on Google's second page of results, but if you Google: fine tuning of the universe, fine tuning of the solar system, or, fine tuning of the earth, Google ranks rsr.org/fine-tuning on its first page!
* Astounding and Unexpectedly Beautiful Equations: E = mc2. Exploring unexpected and even startling symmetry and patterns from the microscopic to the galactic scale, mathematicians often describe their work as an aesthetic pursuit of beauty, as Lacayo quotes Einstein that relativity was his "most beautiful discovery."
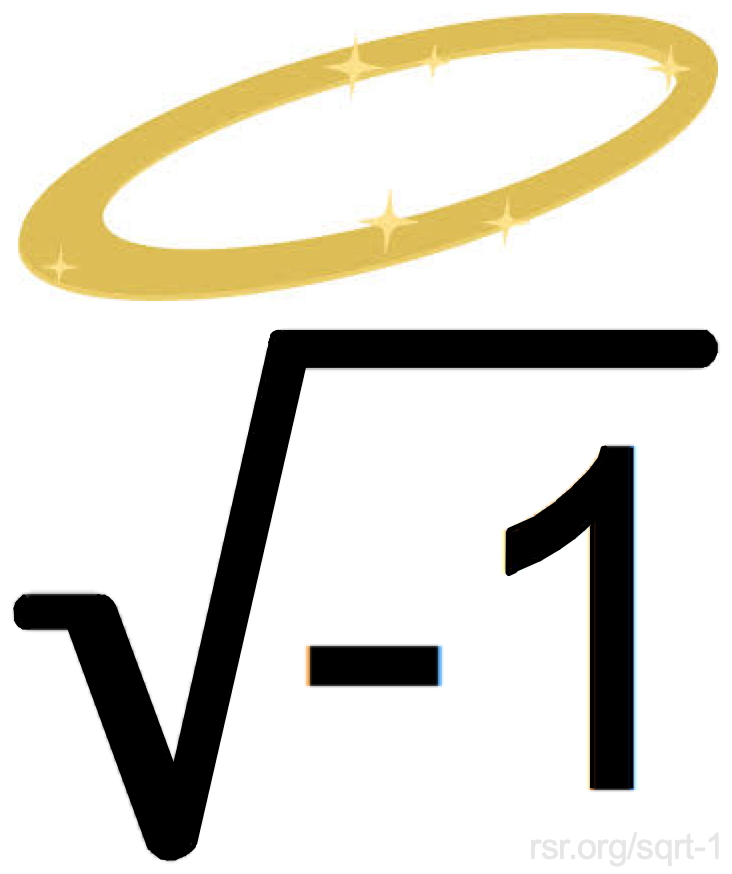
| Symmetry | E | = mc2 |
| Electrons | (i∂ - m)ψ | = 0 |
| Entropy | S | = k log W |
| Propagation | I | = P/(4π r2) |
| Fields | ∇∙B | = 0 |
| Uncertainty | ∇ P ∇x | ≥ ħ/2 |
| Thermodynamics | dS | ≥ 0 |
| Radiation | E | = hf |
| Waves | ψ(x, y, z, t) | = a + ib a |
| Force | F | =ma |
And then there's even complex numbers, and the square root of negative one, which itself is a beautiful conundrum, which govern electric circuits and other areas of quantum mechanics!
What forces obey the inverse square law? Light, gravity, electric fields, sound, radiation. And why say, "Obey"?
And what do we make of the beauty of Dirac's equation, (∂ + m) ψ = 0, describing how fast-moving electrons behave? He himself wrote in Scientific American in 1963, "It seems to be one of the fundamental features of nature that fundamental physical laws are described in terms of a mathematical theory of great beauty", and further, on a blackboard in Moscow, "A physical law must possess mathematical beauty." Consider that scientists enjoy the inverse square law I = P/(4π r2), the beauty of Maxwell's field equations, and of Ludwig Boltzmann's formula for entropy, which is even engraved on his tombstone. And as math becomes increasingly purely theoretical, it seems to do an even better job at describing reality, as with the use of the square root of negative one, not only as in describing electrical circuits in the 1800s, but also today for describing quantum mechanics. Another Ludwig, von Mises, similarly wrote in Human Action, that contemporary philosophers "are entirely wrong in their endeavors to reject any kind of a priori knowledge and to characterize logic, mathematics and [economics] as empirical and experimental disciplines. ... Moreover, it is not experience but thinking alone which teaches us that, and in what instances, it is necessary to investigate unrealizable hypothetical conditions in order to conceive what is going on in the real world" pp. 32, 65.) In the 1820s Carnot could not empirically sense but he did intellectually realize that even an idealized perfect heat engine could never operate at 100 percent efficiency (The Arrow of Time, Coveney & Highfield, p. 149). Like Einstein and Schrödinger, "Galileo is also known for his thought experiments", says Nova. "These are carried out entirely in the mind..." So ignoring their five senses, the mathematicians who turn away from the physical world to the non-material world of ideas, seeking pleasure from pure intellectual elegance, often end up being the ones who come closest to describing the physical nature of the cosmos. Atheists struggle with this phenomena because it suggests that the universe originated with the desire for beauty in the mind of a personal Creator.
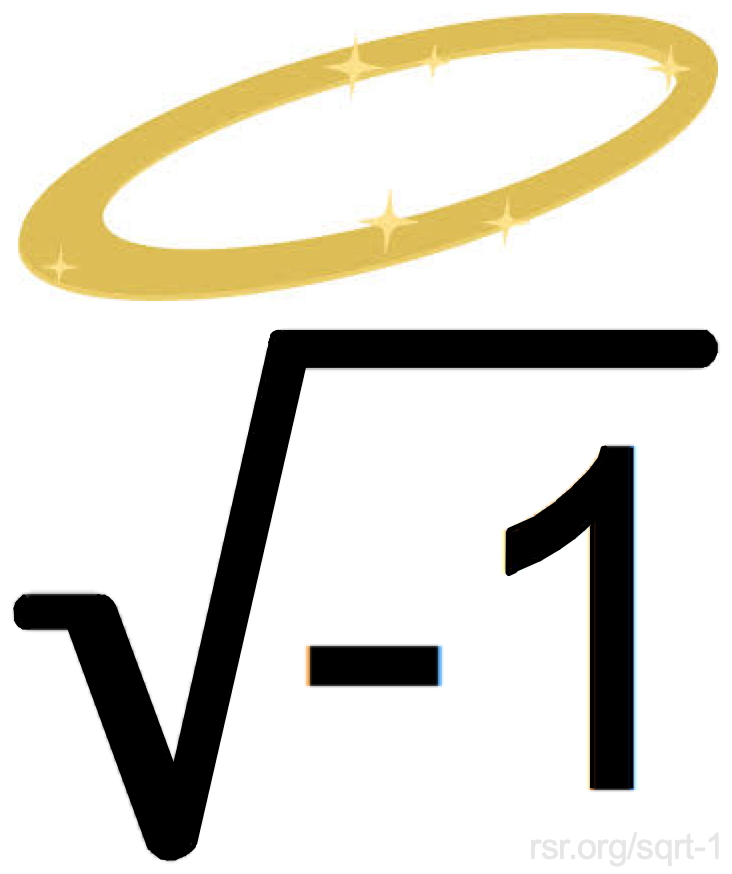* The Square Root of Negative One Reveals the Creator: Using an imaginary number, we achieve improved understanding of the physics of quantum mechanics (as mentioned just above) and of electric circuits (a bit further above). How could that be? The square root of a negative number has no material analog and is only a concept. Therefore only an intellect, heavenly or not, can use imaginary numbers. For arguments sake, we can concede that something like the inverse square law could conceivably arise in a posited big bang materialist "reality". But such a big bang universe would be unable to use the square roots of negative numbers because they are not "real", except that as concepts, they are as real as any other concept. And intellects use "concepts" as design parameters all the time. Cartographers, for example, use imaginary numbers within complex formulas to create sophisticated map projections. When God designed the universe, being the Great Mathematician, He not only used arithmetic but complex, higher mathematical disciplines that He himself had created. God used the imaginary unit, that is, the square root of negative one, in His design. So when human beings, sentient, brilliant, and made in God's image, likewise devised higher mathematical disciplines, they made discoveries including the concept of the imaginary unit and, by their God-given inquisitiveness and creativity, probed the world of physics through the lens of imaginary numbers and found a startling correspondence, such that the use of the square root of negative one gives real insight into the deep physical reality. Because a strictly materialist big bang reality could not utilize a concept such as an imaginary number that has not physical analog, the usefulness of the square root of negative one reveals the Mind of the Creator to us as we explore His cosmos. In a section over at rsr.org/atheism titled Materialists vs. Everything, of the many real things that are not material, we list some of the more substantive ones, including numbers, math, information, codes, the laws of logic, morality, souls, and spirits. And then we ask a question that is yet another potentially devastating issue for materialists: What is matter made of? What if it turns out that matter itself is non-physical? Like biological organisms that are information based more than they are carbon based, if it turns out that matter itself is, like physicist John Wheeler implied, is information based, then materialism is deader than a doorknob. Many struggle to understand Wigner's point in his Unreasonable Effectiveness of Mathematics, and Einstein's point that, "the eternal mystery of the world is its comprehensibility" and that the gap between matter and ideas should be (as a materialist would see it), a "gulf–logically unbridgeable." Those who have the same difficulty as Wigner and Einstein might be able to cross their "gap" as they ponder the implications of the effectiveness in understanding physics by the use of the square root of negative one.
* Mathematics Useless for Moral Truth: Conversely, while math helps man to understand physical reality, it is no use whatsoever regarding moral truth. Moral understanding never involves numbers. As American Right To Life put it in their Albert Einstein: In His Own Words article (extending upon a quote above):
In 1936 Einstein famously wrote, 'the most incomprehensible thing about the world is that it is comprehensible,' and in 1944, remarking about Bertrand Russell, he described the ability to get from matter to ideas as a 'gulf-logically unbridgeable,' which some scientists and linguists refer to as Einstein's Gulf, and in 1950, Einstein wrote that 'science can only ascertain what is, but not what should be,' necessarily excluding from its domain 'value judgments of all kinds.'
Neither math nor science are helpful in establishing moral truth. American Right To Life uses this vital concept in developing their strategy to re-criminalize child killing. The secular humanist utilitarian philosopher John Stuart Mills is frequently paraphrased as calling for the greatest good for the greatest number. Sadly and ironically, the Southern Baptist Convention's chief ethicist Richard Land uses such situational ethics to defend support for funding the killing of some unborn children (for example), in an attempt to save other unborn children. Such utilitarian moral relativism contrasts with the simple biblical command to "obey God" (Acts 5:29), which never requires solving multiple simultaneous equations to determine right from wrong. God does not ask us to calculate arithmetically the number of possible future positive or negative results from our actions. Those actually following Christ would never submit to the criminal who says, "shoot this one in the head and we'll spare those," nor would they support funding the killing of some children to defund the killing of others. Instead of requiring advanced math skills, God refers to entire nations as "children," and gives men commands that even a child could understand. "Do not steal." "Do not bear false witness." "Do not kill the innocent." And don't "do evil that good may come of it." See more at AmericanRTL.org/exceptions#numbers.
* Did Richard Feynman See God? When accepting his Nobel prize in physics, Feynman said, "The fact that electrodynamics can be written in so many ways... was something I knew, but I have never understood. It always seems odd to me that the fundamental laws of physics, when discovered, can appear in so many different forms... An example of that is the Schrödinger equation and the Heisenberg formulation of quantum mechanics. I don't know why this is - it remains a mystery, but it was something I learned from experience. There is always another way to say the same thing that doesn't look at all like the way you said it before. I don't know what the reason for this is. I think it is somehow a representation of the simplicity of nature. A thing like the inverse square law is just right to be represented by the solution of Poisson's equation, which, therefore, is a very different way to say the same thing that doesn't look at all like the way you said it before. I don't know what it means..." Feynman might have been observing yet another manifestation of the one to many solution, that is, the plurality in the Godhead. Perhaps multiple persons of the triune God, each being transcendent, impressed themselves on physical reality. Thus, the biblical truth applies, pun intended, even in physics, that "a matter is established by two or three witnesses." In his book QED (referenced at rsr.org/three), Feynman asks how many fundamental actions are there to account for nearly all phenomena in the universe regarding light and electricity to which he answered: "There are Three!" This reminds us of later in his Nobel lecture where said, "This then is another, a third way, of describing quantum mechanics, which looks quite different than that of Schrödinger or Heisenberg, but which is equivalent to them." And a final observation from Feynman's Nobel prize lecture that reinforces the point of this RSR program, "Dirac obtained his equation for the description of the electron by an almost purely mathematical proposition."
Today’s Resource: Get the Spike Psarris DVD What You Aren't Being Told About Astronomy! Have you browsed through our Science Department in the KGOV Store? Check out especially Walt Brown’s In the Beginning. And you can now get on DVD, Blu-ray, or download, Bob Enyart's The Global Flood and the Hydroplate Theory. Update: Since we first listed this video, it has become RSR's best-selling science resource. As with all of our materials, you'll love it or your money back! So to order, just click above or call us at 1-800-8Enyart.
Online Math Tutorials for Kids (and adults :): To better understand some simple, and more complex, concepts in math, check out BetterExplained.com!
* Mathematics is One of the Languages of God: If you enjoyed RSR Goes To Math Class, you may want to listen to us interview James Nickel, author of Mathematics: Is God Silent? Nickel talks with Bob Enyart about Albert Einstein and how the personal creator God is the answer to the question that Einstein wrestled to answer. Bob and James also talk about Isaac Newton, Johann Kepler, and why science was stillborn in ancient Greece.
* RSR's 50 Years Later Wistar Conference Report: What happened when many of the world's leading mathematicians gathered to evaluate the mathematical feasibility of Darwinism? Check it out at rsr.org/wistar.
* Bob Enyart falls victim to spam entrapment: (Warning: As is typical and unfortunately at this RationalSkepticism.org site also, beware the filthy language of the evolutionary forums, where many participants have a hard time communicating without repeated reference to human waste and reproduction.) On June 6, 2014 Bob began reporting on his interacting with a dozen atheists at RationalSkepticism.org on a thread about their belief in the evolution of the eye. See the whole sordid affair at rsr.org/rational-skepticism! :)
* RSR Friend Andy McIntosh's Math Webinar: On Monday, Oct. 13, 2014 at 1 p.m. E.T. with many in the UK and the US, Bob Enyart will be watching Science, Mathematics and Beauty.
The power of mathematics is a very strong argument for the existence of the transcendent God. We will first consider the nature of abstract thought. We will then consider the nature of mathematics and its connection to reality... that meaning and purpose are realities which are transcendent to the physical Universe.
This talk will deal with... the intriguing beauty and power of mathematics. ... When used to describe the physics of one system it is surprising how many other disciplines reflect the same principles so that the form of the equations can be similar. But we need to start with an even more fundamental concept concerning number itself. As Dr. Jason Lisle has said,
"Numbers are concepts. Thus they are abstract in nature. They exist in the world of thought and are not material or physical. You cannot literally touch a number, or even see one, because they are not made of matter."
* On the Claim that Math is Not Science: Those who make many self-contradictory claims including that nothing can be certain have a hard time defending their assertion that math is not science. Their case might be stronger if there were definitive answers to the questions, What is mathematics and What is science? For example, scientists along with philosophers of science wrestle with the demarcation problem, of defining what science essentially. Because the mathematics, philosophical, and scientific communities have not resolved the definitions of science and math, and because math is a discipline central to science, a dogmatic assertion that math is not science appears to be unjustified. Some claim that math is not science because it's not empircal, that is, because it's not based on sensory observation. But which of the five senses tell us that science must be based on the senses? Whether the lack of empiricism claim were valid or not, the very claim itself should lead its proponents to also conclude that it is unscientific to claim that science requires observation. Because observation (empiricism) cannot validate the unscientific claim that science requires observation. (See RSR's rebuttal to Atheist Cliché #4.) On the contrary, just as it requires knowledge of origins to accurately define what a species is (or technically, what a kind is) and what a planet is, so too the only objective definition of science (and mathematics) depends on the unbiased view of Jesus Christ, the Great Mathematician Himself.