* RSR Interviews a UC San Francisco Professor of Ophthalmology: [Update: To hear RSR's 2014 analysis of this debate, go to rsr.org/eye-evolution.] Real Science Radio co-host Bob Enyart debates clinical professor of ophthalmology Dr. Gary Aguilar on the evolution of the eye. Six months ago Gary recommended that Bob read a 2012 book by Dr. Schwab, a colleague of Aguilar's at UC Irvine, about which Russell Fernald says that Evolution's Witness is "likely to be consulted by everyone interested in evolution and eyes." Hear that 40-minute debate about the eye by clicking any of our standard audio links above, or click here for an 83-minute wide-ranging discussion that also addresses many non-science issues.
* RSR Interviews a UC San Francisco Professor of Ophthalmology: [Update: To hear RSR's 2014 analysis of this debate, go to rsr.org/eye-evolution.] Real Science Radio co-host Bob Enyart debates clinical professor of ophthalmology Dr. Gary Aguilar on the evolution of the eye. Six months ago Gary recommended that Bob read a 2012 book by Dr. Schwab, a colleague of Aguilar's at UC Irvine, about which Russell Fernald says that Evolution's Witness is "likely to be consulted by everyone interested in evolution and eyes." Hear that 40-minute debate about the eye by clicking any of our standard audio links above, or click here for an 83-minute wide-ranging discussion that also addresses many non-science issues.
* Ivan Schwab's Evolution's Witness -- How Eyes Evolved: Within minutes of the mailman delivering this book, on March 31, 2012, Bob wrote on the title page, with a number of folks around him signing as witnesses: "Prediction: Very little of this book will be about how eyes evolve." Dr. Aguilar described this textbook as a "tour de force" showing clearly how eyes evolved. During today's interview, Bob asserts that his prediction was valid, and that 99% of this book has nothing to do with how eyes evolve. It's a great anatomy book though!
* The Opsin Missing Chapter: Opsin is the protein in photoreceptor cells that can detect a single photon and then signal that a photon has struck it. One might expect from a book on the eye's evolution, that after a book's introduction, the author might include a chapter on an explanation, conceptually, of how opsin might evolve. In vertebrates and invertebrates, opsin requires a chain of 150 to 250 amino acids, which then must be folded correctly into a very specialized nano-machine which can pass along an output signal whenever the protein gets hit with a single photon. But, as creationists would expect, no such chapter exists in the book. And actually, all the difficult problems that one would have to address if he were actually writing a book on "How eyes evolved," do not appear in the book.
 * The Vision Challenge Missing Chapter: Bob Enyart brought up this vision challenge to Gary Aguilar, but, like most atheists and evolutionists we've discussed this with, Gary was unresponsive. It appears that atheists and evolutionists do not even know how to think about this problem, let alone can they offer any conceivable notion about how it could even theoretically be solved. See this vision challenge presented in full from our debate with TheologyOnline.com's resident atheist Zakath. Bob had predicted that even a state-of-the-art "tour de force" textbook by an ophthalmology professor would not even begin to describe how vision might evolve, and also, that this interview with an ophthalmologist professor would demonstrate their basic inability to substantively think through something that they routinely oversell to the public as a done deal. "We know 'how eyes evolved,' only an ignorant person would doubt our claims." At 2:33 into an interview on The Evolution of the Eye, Richard Dawkins illustrates the RSR "APPtitude test," aka, the Atheist Popularity Postulate, that the evolutionists who become the most popular are the ones who say the most absurd things with the straightest face. Imagine his evolving, curling, sheet of light-sensitive paper sending a static-like data stream to an unwitting brain that must then interpret the predator's shadow or direction of light (from the data represented by the screen above, on the left).
* The Vision Challenge Missing Chapter: Bob Enyart brought up this vision challenge to Gary Aguilar, but, like most atheists and evolutionists we've discussed this with, Gary was unresponsive. It appears that atheists and evolutionists do not even know how to think about this problem, let alone can they offer any conceivable notion about how it could even theoretically be solved. See this vision challenge presented in full from our debate with TheologyOnline.com's resident atheist Zakath. Bob had predicted that even a state-of-the-art "tour de force" textbook by an ophthalmology professor would not even begin to describe how vision might evolve, and also, that this interview with an ophthalmologist professor would demonstrate their basic inability to substantively think through something that they routinely oversell to the public as a done deal. "We know 'how eyes evolved,' only an ignorant person would doubt our claims." At 2:33 into an interview on The Evolution of the Eye, Richard Dawkins illustrates the RSR "APPtitude test," aka, the Atheist Popularity Postulate, that the evolutionists who become the most popular are the ones who say the most absurd things with the straightest face. Imagine his evolving, curling, sheet of light-sensitive paper sending a static-like data stream to an unwitting brain that must then interpret the predator's shadow or direction of light (from the data represented by the screen above, on the left).
 * Evolution Misled Eye Expert About the Eye: Gary Aguilar repeatedly claimed that the plica semilunaris (in the corner of your eye) is a functionless leftover of evolution. For example, at 3:15 into our interview, he said, "There are aspects of the human eye, for example, the nictitating membrane [which in some creatures is an additional, transparent eyelid] in lower animals is present in the plica semilunaris which has no function in humans; none whatsoever." Then to Bob's question, "Dr. Aguilar, can you repeat that, what is it that has no function whatsoever?" Gary answered, "The plica p-l-i-c-a semilunaris." However, according to the authoritative Duane's Foundations of Clinical Ophthalmology (Vol. 2, Ch. 2: Plica Semilunaris), the plica functions during movement of the eye, to help maintain tear drainage, and to permit greater rotation of the eyeball, for without the plica, the membrane called the conjunctiva would attach directly to the eyeball, restricting movement. Gary here illustrated something we describe about evolutionists, that rather than being informed with the latest knowledge from his own area of expertise, Aguilar claimed decades out of date "evidence", in his case, on the anatomy of both the wiring of the retina, and on the plica, claiming it is a functionless leftover. Rather than researching his Darwinian claims in the most relevant scientific literature, Aguilar, following Dawkins, ultimately got his outdated claims from a 150-year old book by Charles Darwin. Aguilar also repeats Dawkins' long-refuted claim, based on scientific ignorance and evolutionary bias, that the human eye is wired backward. For an explanation of why our eye is wired the reverse of an octopus, and optimally for human vision, listen to the Enyart-Aguilar-Eye-Excerpts, and see Dr. Carl Wieland's article, and a paper by Peter Gurney, a fellow of the Royal Colleges of Ophthalmologists in a peer-reviewed creation journal, as well as Gurney's popular article that deals with both the plica and the wiring. And read and hear Dr. Jerry Bergman explain that the function of the plica semilunaris has been documented since the 1930s. 2013 UPDATE: Dr. Aguilar wrote to Bob Enyart, "...let me acknowledge that the plica semilunaris is considered to have some function..." though he denied the plica aids in globe movement, thereby apparently disagreeing with the statement in Duane's Ophthalmology that, "if the conjunctiva were to directly join the eyelids to the globe, the globe and eyelids would both be restricted in movement." Perhaps Gary could share his disagreement with DO's Darlene Dartt and help everyone get to the bottom of that one particular detail.
* Evolution Misled Eye Expert About the Eye: Gary Aguilar repeatedly claimed that the plica semilunaris (in the corner of your eye) is a functionless leftover of evolution. For example, at 3:15 into our interview, he said, "There are aspects of the human eye, for example, the nictitating membrane [which in some creatures is an additional, transparent eyelid] in lower animals is present in the plica semilunaris which has no function in humans; none whatsoever." Then to Bob's question, "Dr. Aguilar, can you repeat that, what is it that has no function whatsoever?" Gary answered, "The plica p-l-i-c-a semilunaris." However, according to the authoritative Duane's Foundations of Clinical Ophthalmology (Vol. 2, Ch. 2: Plica Semilunaris), the plica functions during movement of the eye, to help maintain tear drainage, and to permit greater rotation of the eyeball, for without the plica, the membrane called the conjunctiva would attach directly to the eyeball, restricting movement. Gary here illustrated something we describe about evolutionists, that rather than being informed with the latest knowledge from his own area of expertise, Aguilar claimed decades out of date "evidence", in his case, on the anatomy of both the wiring of the retina, and on the plica, claiming it is a functionless leftover. Rather than researching his Darwinian claims in the most relevant scientific literature, Aguilar, following Dawkins, ultimately got his outdated claims from a 150-year old book by Charles Darwin. Aguilar also repeats Dawkins' long-refuted claim, based on scientific ignorance and evolutionary bias, that the human eye is wired backward. For an explanation of why our eye is wired the reverse of an octopus, and optimally for human vision, listen to the Enyart-Aguilar-Eye-Excerpts, and see Dr. Carl Wieland's article, and a paper by Peter Gurney, a fellow of the Royal Colleges of Ophthalmologists in a peer-reviewed creation journal, as well as Gurney's popular article that deals with both the plica and the wiring. And read and hear Dr. Jerry Bergman explain that the function of the plica semilunaris has been documented since the 1930s. 2013 UPDATE: Dr. Aguilar wrote to Bob Enyart, "...let me acknowledge that the plica semilunaris is considered to have some function..." though he denied the plica aids in globe movement, thereby apparently disagreeing with the statement in Duane's Ophthalmology that, "if the conjunctiva were to directly join the eyelids to the globe, the globe and eyelids would both be restricted in movement." Perhaps Gary could share his disagreement with DO's Darlene Dartt and help everyone get to the bottom of that one particular detail.
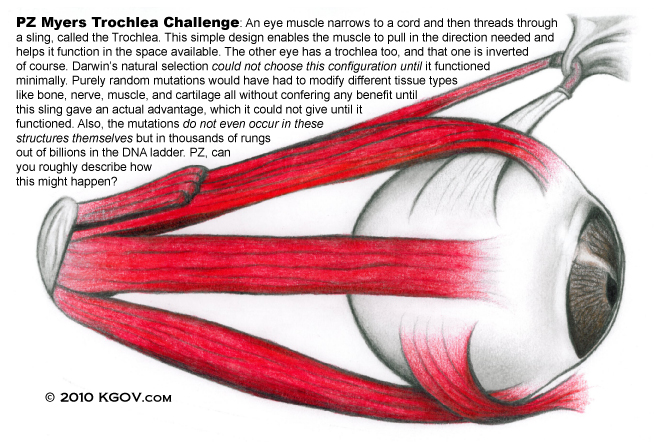
* The Missing Trochlea Challenge Chapter: Ivan Schwab doesn't include a chapter on how simple mechanics of the eye would have evolved, as illustrated in this trochlea challenge which has been circulating on the web in evolution circles from well before Schwab's book was published. Back on April 18th, we sent to Gary our PZ Myers Trochlea Challenge. It's this simple sketch of the human eye, with a single question in its caption. PZ has responded to us, admitting that he cannot answer this challenge, and we appreciate that truthfulness.
* For More About PZ and this Trochlea Challenge: See realscienceradio.com/PZ for PZ's response. And for a full presentation of this challenge, please see our debate on Entropy and Evolution that was prompted by an American Journal of Physics paper by Prof. Dan Styer (in which Styer himself joined in). Bob Enyart presented the trochlea challenge in detail explaining why evolution could not bring about something even as conceptually simple as the trochlea. And of course, if evolutionists can't explain how the trochlea would form, they certainly cannot explain, and therefore take by faith, that stationary eyes somehow evolved into eyeballs that could move up and down and from side to side.
* The Richard Dawkins Dichromatic Challenge: Consider an organism which can see in black and white, and then estimate the necessary steps required to modify it to incorporate color also, sufficiently well to give it a survival advantage. Of course, until the dichromatic vision confers a survival advantage, natural selection cannot guide the development of dichromatic vision. Gary Aguilar never got around to acknowledging this problem, let alone, like his colleague Schwab, attempting an answer. In the forward to Schwab's book, Dr. Fernald echoes Dawkins' "Climbing Mount Improbable" (one of Dawkins' many books which he later admitted provide no evidence for evolution), affirming that for eyes to evolve, they would have had to proceed from the accumulation of many tiny steps. Fernald writes that a "complex eye could be formed by natural selection," quoting Charles Darwin, only by "numerous gradations" in which "the eye does vary ever so slightly..." If, however, there are no logical or physiological small steps that are even theoretically possible, between a black-and-white type monochromatic system, as compared to a color vision system, then that would present a hurdle that neo-Darwinism could not cross. For the obvious survival advantage that would come from seeing in both black and white and in dichromatic color requires:
- the detection of black and white (monochromatic) along with a range of color light waves
- the transmission to the brain over an optic nerve of a dichromatic, rather than only a monochromatic, data stream (similar to the problem of trying to watch in real time a broadband HD video over an old-fashioned dial-up 2400 baud modem)
- an integration of the ever-changing monochromatic image with the color image, a non-trivial data processing feat.
Of course, and this is virtually a tautology that cannot be rationally rejected, if there is no logical or physiological step between seeing in "black and white" and in adding an additional channel of red, green or blue hues, then this challenge alone refutes Darwinism. RSR asserts that this is, in fact, the case, and that this observation falsifies evolution.
* In Contrast to Serious Discussion, Look at Dawkins Describe Eye Evolution: Watch about one minute, beginning at 2:09 in to this friendly interview of Richard Dawkins on the evolution of the eye. His encapsulation of wild required complexity into absurd superficiality is common among evolutionists. Consulting Fernald, Aguilar, and Schwab makes it clear that Dawkins is being superficial, not because he's pressed for time in a popular interview, for Schwab takes 300 pages in a college-level "tour de force" textbook allegedly dealing with "how eyes evolved," and never gets beyond Dawkins' sheet-cupping superficiality.
* Bob Banned in Bavaria By a Bunch of Believers: Was Bob the victim of entrapment, specifically, of spam entrapment? :) A group of atheists (people who believe deeply that nothing created everything, that life arose from non-life, etc.), at RationalSkepticism.org ran out of tolerance for Bob Enyart by his 27th post on their forum. Get the links and see the story below.
* Carbon 14 in Diamonds and Dinosaur Bones: Early in the program Gary Aguilar could not understand how short-lived Carbon 14 might even theoretically be able to be used to falsify a claim that a particular specimen might be a million years old. Then at about 36 minutes in he challenged Bob: I want you to find me a credible scientist who says that because of Carbon 14 in diamonds, that they are therefore less than 7,000 years old. Because of the work of physicist Russell Humphreys, Bob was able to answer, "How about a scientist at Sandia National Labs, who has published on this?" See more at realscienceradio.com/14c. And as to Gary saying that Bob didn't answer his question about Mary Schweitzer, see our DinosaurSoftTissue.com. When Gary asked, "Why can't you convince Mary (that extant dinosaur blood vessels, osteocytes, blood cells, etc., indicate that dinosaurs lived only thousands of years ago)?" Bob tried to explain that one human being cannot convince another of anything against their will (of course). And Bob thought that Gary would get his point when he said that paleontologists like Mary have ignored that short-lived Carbon 14 is everywhere it shouldn't be, including in diamonds and dinosaur bones.
 For today's show Real Science Radio recommends
For today's show Real Science Radio recommends
Dr. Carl Werner's DVDs, Living Fossils and
its prequel Evolution, the Grand Experiment!
Today’s Resource: Get the fabulous Carl Werner DVD Living Fossils and his great prequel, Evolution: The Grand Experiment! And have you browsed through our Science Department in the KGOV Store? Check out especially Walt Brown’s In the Beginning! Also, you can consider our BEL Science Pack; Bob Enyart’s Age of the Earth Debate; Bob's debate about Junk DNA with famous evolutionist Dr. Eugenie Scott; and to give as a Christmas or birthday gift, the superb kids' radio programming, Jonathan Park: The Adventure Begins!
* Bob Too Slowly Replied to Gary's Moon Crater Question: Gary Aguilar was correct that Bob took too long to get around to answering his claim that all the craters on the moon are themselves proof of the passage of millions of years. Bob answered that because the near side of the moon has far more maria, or ""seas," which are the result of massive impactors, than does the far side, that this should help people realize that there is something wrong with the old-earth explanation of how those craters got there. Further, Bob never got around to explaining how NASA has learned, from inspection of a moon of Jupiter, that second-hand craters, that is, craters formed by debris thrown up by the impact of other craters, accounts for 95% of small craters and a significant percent of medium-sized craters. So, if the leading Big Bang cosmologists were committed to the data, or even to their theories, they would agree that therefore, the crater evidence on the moon suggests that it is significantly younger than they had previously claimed. For more, see our favorite astronomy DVD: What You Aren't Being Told About Astronomy! However, the ultimate commitment of the prevailing Darwinist and old-earth science communities is NOT the Big Bang, or descent with modification, etc., but atheistic materialism.
* Hear the Full Version: The Gary Aguilar interview lasted three times longer than a typical RSR program so we provide here the 83 minute rambling version. Bob enjoys an informal conversational approach with both parties casually interrupting each other, whereas in a temper tantrum Gary insisted that Bob remain silent until Gary ceased talking. And even though Gary received more than half the air time, he repeatedly complained that he wasn't getting equal time. Gary's boorish behavior made for boring radio, but we provide this audio regardless in part so that parents can hear what their children will find at a typical state university. We assume that Dr. Aguilar is an accomplished surgeon, but with his inability to think clearly, his advocacy of pot, his bad behavior, and his rage against Christians, his patients might want to consider seeing a more professionally behaved surgeon.
* Gary's "Good Christians": Dr. Aguilar recognizes that there are many Christians who believe like he does on many topics, including legalizing cocaine, belief in Darwinism, and holding an anti-Israel foreign policy. So, when he says, "good Christian," as he does often, one might think that he was referring to these Christians whom he agrees with. However, Gary never does that. He only uses the phrase "good Christian" when he refers to someone called a Christian who murdered, plundered, raped, etc. Then at about 52 minutes in, Gary, upset at Bob for opposing the decriminalization of heroin, crack, etc., said of Bob and of people like him, "You need to be set aside."
About 52:30 into the show, Bob asks Gary if it is possible that his anger toward Christians causes him to be biased to automatically agree with Darwinists about evolution. He emphatically denied this: "I give no thought whatsoever to evolution or Darwinism." So, if Gary doesn't think about evolution, yet believes in it unequivocally, even to defending its strongly refuted arguments (like the backwardly-wired eye), there must be something that is biasing him in that direction. It just seems that his intense anger toward "Good Christians" might be the source of his bias.
* Bob Enyart falls victim to spam entrapment: (Warning: As is typical and unfortunately at this RationalSkepticism.org site also, beware the filthy language of the evolutionary forums, where many participants have a hard time communicating without repeated reference to human waste and reproduction.) On June 6, 2014 Bob began reporting on his interacting with a dozen atheists at RationalSkepticism.org on a thread about their belief in the evolution of the eye. See the whole sordid affair at rsr.org/rational-skepticism! :)