* For the History of Base 60: see below.
* Different Sides of the 360/365 Day Question: Hear Real Science Radio's Bob Enyart interview Dr. Faulkner. The long-time University of South Carolina Astronomer Danny Faulkner is now full time with Ken Ham's ministry, Answers in Genesis at the Creation Museum (near Cincinnati). With a Ph.D. in astronomy from Indiana University Dr. Faulkner, is also a board member of the Creation Research Society.
* Was the Year Once 360 Days Long? In Dr. Faulkner's CRSQ paper, (rebutted, also in CRSQ, by Enyart), Danny argues against the widespread belief among many creationists (including Henry Morris and Walt Brown) that God originally created the Earth with a 360-day year and 30-day months. (Morris' organization, ICR, the Institute for Creation Research, thankfully continues to teach the created 30-day month and 360-day year.) Enyart offers to Dr. Faulkner evidence to counter his disagreement with the idea, and the two agree to evaluate additional original source material from ancient civilizations and perhaps to do a follow up program on the matter.
For this program RSR recommends The Young Sun
DVD with Danny Faulkner and other great astronomers!
2017 Update on 360DayYear.com: You've just GOT TO CHECK OUT this amazingly informative and fun website! As promised, Bob Enyart has been posting historical and scientific evidence suggesting a 360-day year. You can check it out online at 360dayyear.com! Also, you may want to check out the second of three objections to Walt Brown's hydroplate theory, at RSR's List of Answers to Hydroplate Objections.
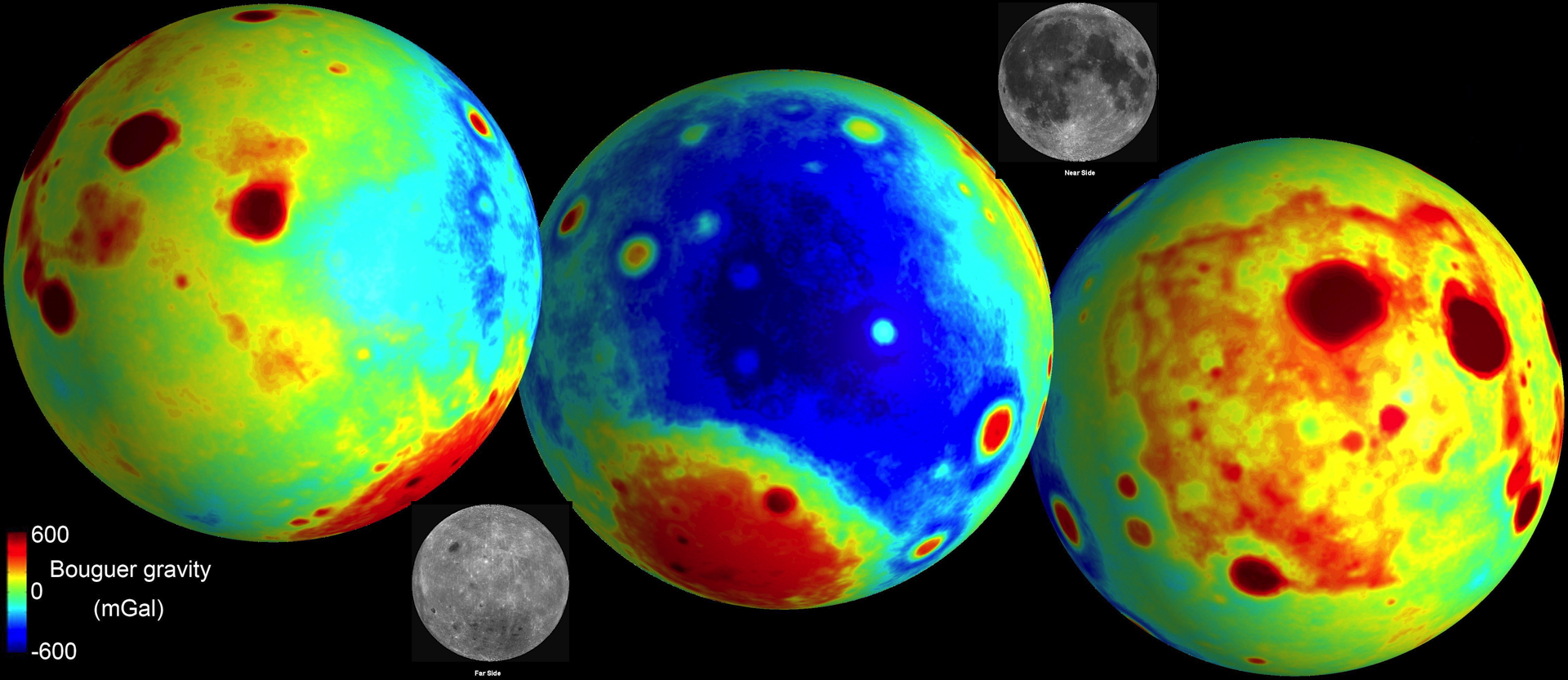
 * What Makes One Side of the Moon 1) Heavier and 2) the Near Side? Both questions have one answer. It's the mascons (mass concentrations). Explaining why a U.S. lunar satellite unexpectedly crashed, NASA's Alex Konopliv said, "The Moon is extraordinarily lumpy, gravitationally speaking... in mass. What appear to be flat seas of lunar lava have huge positive gravitational anomalies—that is, their mass and thus their gravitational fields are significantly stronger than the rest of the lunar crust." And NASA continued, "Known as mass concentrations or 'mascons,' there are five big ones on the front side of the Moon facing Earth, all in lunar maria (Latin for 'seas')," including the pareidolic "Man in the Moon" facial features. And, "The mascons' gravitational anomaly is so great—half a percent" [!] that astronauts could have easily noticed it "standing at the edge of one of the maria, a plumb bob would hang about a third of a degree off vertical, pointing toward the mascon." Wow!
* What Makes One Side of the Moon 1) Heavier and 2) the Near Side? Both questions have one answer. It's the mascons (mass concentrations). Explaining why a U.S. lunar satellite unexpectedly crashed, NASA's Alex Konopliv said, "The Moon is extraordinarily lumpy, gravitationally speaking... in mass. What appear to be flat seas of lunar lava have huge positive gravitational anomalies—that is, their mass and thus their gravitational fields are significantly stronger than the rest of the lunar crust." And NASA continued, "Known as mass concentrations or 'mascons,' there are five big ones on the front side of the Moon facing Earth, all in lunar maria (Latin for 'seas')," including the pareidolic "Man in the Moon" facial features. And, "The mascons' gravitational anomaly is so great—half a percent" [!] that astronauts could have easily noticed it "standing at the edge of one of the maria, a plumb bob would hang about a third of a degree off vertical, pointing toward the mascon." Wow!
* What Made the Mascons the Mascons? So the reason the near side of the Moon is the near side is because it is heavier than the far side so Earth's gravity holds the near side closer. Far more massive impacts hit the near side, making those areas 1) heavier, and 2) flatter, because those areas became molten from the massive and high-energy impacts, in the process erasing many thousands of craters. (That's why the much less beat-up far side is sprinkled with so many more craters, number-wise, but not mass-wise, because they weren't erased by the once-molten mascons.) On today's program, Bob Enyart shares with Dr. Faulkner NASA's most recent gravity mapping of the Moon, by which they created the above Bouguer gravity map. This map appears to provide evidence that is consistent with the Hydroplate Theory's explanation for how the near side of the Moon became so much heavier (with its greater mass concentrations). So the most massive impacts melted away thousands of craters, left huge dark maria in their place, and then with all that extra mass have kept that side of the moon (though with dramatic libration) as the Earth's near side.
* Ancient Use of Base 60 and the 360 Day Year: The ancient Sumerian word for the number 60 is geš and the English word for Base 60, from sexagesimus which is the Latin for sixtieth, is sexagesimal. Robert K. Englund, Ph.D., UCLA prof. of Assyriology & Sumerology, Administrative Timekeeping in Ancient Mesopotamia, Journal of the Economic and Social History of the Orient, 1988, pp. 121-122:
The sexagesimal system of counting... is attested in periods much earlier than any secure attestation of the Sumerian language, namely in the periods Uruk IV-III [~3200 B.C.], and possibly in some token assemblages from clay envelopes unearthed in levels of proto-elamite Susa corresponding to Uruk V [~3400 B.C.]. ... A mixture of this sexagesimal system with a heritage of natural cycles [the lunar and solar orbits] resulted in the 3rd millennium time divisions attested by administrative documents. ... The resulting system... which without question complemented throughout the 3rd millennium natural, lunisterllar divisions, is attested in its basic form of a twelve-month, 360-day year in the archaic documents from the end of the 4th millennium [B.C.].
Question for the Audience: What numerical base is the first
known in recorded human history? Is it base 10? Or base 60?
Consider the Sumerian Anomaly just below and rsr.org/origin-of-language.
Please email your thoughts and evidence to Bob@rsr.org.
Englund writes of a Vincenzo Formaleoni that "he was convinced that at the time of the [global] deluge—and the inception of the sexagesimal system—the year was exactly 360 days long" and quotes his Sources of errors in cosmography and geographia of the Ancients, Venice, 1789:
The length of the year was therefore undeniably of 360 days at the time of the first gazers.
Englund cited this quote from the paper, Sketch of a history of the sexagesimal system, by F. Thureau-Dangin, Osiris 7, Paris, 1939, which paper begins as follows:
With the Greeks, and then with the Arabs, the sexagesimal system has been an academic system of numeration, used by the astronomers. We still avail ourselves of this system for the measurement of arcs or angles and for the measurement of time. Save for some rare and late exceptions, (1) this system has, beginning with the Greeks, always been employed to express fractions only. Prior to that, however, in Babylonia, it served to express the integers as well as the fractions. It was a complete system of numeration, used by the Babylonian mathematicians or astronomers. Already at the beginning of Assyriology, examples of the system have been found by the first decipherers: Hinks found some on an astronomical tablet coming from the excavations of Nineveh (2)... Since then, the excavations made in Babylonia, especially those of Sarzec at Tello, have taught us that, before becoming an academic system, the sexagesimal system had been the common and exclusive mode of numeration with the Sumerians, that is, with the predecessors of the Babylonians.
Also Thureau-Dangin, p. 98, summarizes Moritz Cantor's conclusion (with which RSR concurs, though Cantor himself, perhaps glimpsing its implications, later abandoned), from his Vorlesungen ueber Geschichte d. Mathematik (1880, p. 83) that:
The year, which was given the round number of 360 days, gave rise to the circle of 360 degrees, and the division of the circle into six parts, suggested by the fact that the chord of the inscribed hexagon is equal to the radius, gave rise to the number 60, the basis of the system.
* The Sumerian Numbers and the Base 60 Anomaly: See from pages 101, 102, and 103 of Thureau-Dangin's Sketch:



* Two Similar Anomalies a World Apart: Consider also the Mayan numerical anomaly, where midstream they modified their base 20 numerical system, switching in the third place from what would have been 400 to instead 360. (1, 20, 360, 7200, 144,000; i.e., 1 x 20 x 18 x 20 x 20), to pay homage to their 360-day year heritage. (And, consider the French phrase, "I would not say that to you thirty-six thousand times" and the popular "voir trente-six chandelles".) Thureau-Dangin, p. 103, adds:
If, in spite of the so common tendency to take 6 or 12 as a new unity, no system of numeration has been constructed on the base of 6 or on the base of 12, it is due to the fact that man has always counted upon his fingers [RSR: as God of course designed him to do], and that the base imposed upon him since immemorial times [RSR: no such times; for the world remembers Adam] through this mode of counting [in footnote (19) here it is acknowledged that this mode of counting would justify also use of base 20] has come to occupy an almost impregnable position in numeration. Incapable of replacing the decimal scale, the bases of 6 and 12 could only be introduced into numeration in the form of a combination with the base of 10.
With the German peoples, 120 was about to assume the name and the place of 100. [RSR: As in 12 months x 10?] On this question... The facts are... very completely and exactly described. [Thureau-Dangin disagrees though with another scholar's opinion, a J. Schmidt, that in this the Germany's influence had come indirectly from Babylon.]
* Sumer, Babylonia, and Brilliance: The city of Babel was built by Noah's great-grandson Nimrod in what today is southern Iraq. Eventually one of the earliest identifiable people groups, the Sumerians, occupied this region of the Middle East. Their land and culture was later absorbed into the Babylonian Empire. (The initial Babylonian Empire flourished in the second millennium B.C. a thousand years before Nebuchadnezzar and the other kings of the later revived Neo-Babylonian Empire.) Consistent with the increasingly acknowledged genius of ancient man, consider from the University of St. Andrews in the UK that a thousand years before Pythagoras, the Babylonians knew the "Pythagorean" Theorem. And a 2016 paper in the journal Science, Ancient Babylonian astronomers calculated Jupiter’s position from the area under a time-velocity graph, describes the Neo-Babylonian use of a rudimentary calculus a millennium and a half before such calculations were thought to previously have been discovered. Commenting on the paper, Caltech's Noel Swerdlow said of the Babylonians, "They were very, very smart, and the more we learn of what they did, the more impressive, the more remarkable it becomes." And New York University's Alexander Jones added that their work, "testifies to the revolutionary brilliance of the unknown Mesopotamian scholars who constructed Babylonian mathematical astronomy."
* 60 was Unity in Babylon: The University of St. Andrews also reports that:
"The Babylonians divided the day into 24 hours, each hour into 60 minutes, each minute into 60 seconds. ... Two tablets found at Senkerah on the Euphrates in 1854 date from 2000 BC. They give squares of the numbers up to 59 and cubes of the numbers up to 32. The table gives 82 = 1,4 which stands for
82 = 1, 4 = 1 × 60 + 4 = 64
and so on up to 592 = 58, 1 (= 58 × 60 +1 = 3481)."
The two Babylonian names for the number 60 were "geš" and "gešta" the second of which appears to have been a composite of "geš" and "šita" which means "number" (Thureau-Dangin, p. 105), with the name of the number 1 being, apparently, also "geš". And back to Thureau-Dangin, p. 105, "In adopting the habit of designating 60 as "1," the Sumerians were undoubtedly prompted by a conception of 60 as of the (great) unit... the cipher presenting the number 60 looks like the cipher for the unity, but is bigger in size. [Further] One said geš-2 for 120, geš-3 for 180 and so on up to geš-10, that is geš-u, for 600. ... geš-u-2 for 1200, geš-u-3 for 1800, etc. The word designating 602 (or 3600) was šar, a "whole, totality". Footnote (22) then follows: "The original meaning of the word [šar] may have been 'circle.'" And p. 106 shows that the cipher that equaled 3,600 or šar was impressed into a clay tablet by the end of a hollow reed, making the form of a circle.
* 60 was Money in Babylon: Sixty shekels made one mina, and sixty minas made one talent. The Sumerians had also used these measures. Eventually the Greeks adopted the same ratio of 60 minas to one talent. For the Hebrews, whereas Ezekiel indicated that a mina equaled sixty shekels (Ezekiel 45:12), more anciently, rather than using the Sumerians 3,600 shekels in a talent, the Israelites in the wilderness used 3,000, as determined by the accounting described in Exodus 38.
* 60 was Trigonometry in Babylon: Beating the Greeks to trigonometry by 1500 years, because the Babylon's used a sexigesimal system, trigonometry was easier to use. Because today we use tables with approximations and their base 60 was evenly divisible by the three (think triangles), according to the journal Science, ancient Babylonian calculations were even more accurate than those we make with today's trigonometry and computers.
* The Seleucids from Uruk and Divisions of the Day: RSR notices that the fractional divisions of the day, from Thurea-Dangin pp. 109-110, are all in the list of the divisors of the highly composite number 360: "Contracts of the times of the Seleucids, coming from Uruk, refer to the sale of shares in the benefits connected with the exercise of a function... determined by fractions of a day, being such and such a day in the month. The fraction of the day is, for instance, 'one-sixth and one-ninth of the day'... or 'one-sixth, one-eighteenth and one-sixtieth of a day'... or 'one-thirtieth and one-third of one-sixtieth of a day' [i.e., 1/180th]... These successions of unit fractions remind us of the Egyptian system."
* The Akkadians and the Number 60: Unfinished. RSR work in progress...
* Ancient Measurement Affinities for Factors & Multiples of 60: Before we list those measurements, let's remind ourselves about the number 360 being a highly composite number , which is one of the reasons why God would have made with a year comprised of that many days. So to recall its factors, see this from 360dayyear.com#ecliptic:
360 is divisible by many numbers including those especially helpful (in bold, even today) for calendars and timekeeping: 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, and 180. A year of 360 days is reasonably divisible even by the 2 equinoxes, 2 solstices, four seasons, 12 months, etc., 24 hours in a day, 24 time zones of 15 nominal degrees each, 60 minutes in an hour, 60 seconds in a minute (and consider also our comfort with a "dozen" and with 12 inches in a foot and 36 inches in a yard).
* The Measurements: For convenience measuring systems use many varying units. However ancient cultures appeared to have had a tendency to use sexagesimal factors. The following units of measurement are easily found in charts in chapter three of Springer's 2003 Encyclopedia of Scientific Units, Weights and Measures: Their SI Equivalences and Origins.
- Ancient Hebrews: had fundamental units of weight that included 6, 60, 600, 6,000, and 36,000, as well as 12, 24, 48, and 12,000. The ancient Jews also had fundamental units of dry capacity that included 3, 18, and 180 and liquid capacity of 6, 12, and 60.
- Ancient Chinese: had units of area that included 60, units of weight that included 24, 30, and 120; units of length that included 6, 12, 18, 30, 60, 180, 360, 1200, 1440, 1800, 3600, 4500, and 144,000.
- Ancient Indians: units of length that included 12 and 24.
- Ancient Persians: units of area included 144, 1440, 14400, and 144,000.
- Ancient Egyptians: units of length included 3, 6, 12, 18, 24, 30, 72, 120, 144, 300, 3000, 12000, and 30000; and units of weight included 6, 60, 300, 600, 1200, 3000, 30000, and 60000; and units of capacity include 6, 24, 60, and 240.
- Ancient Greeks: units of length include 6, 12, 18, 24, 30, 60, 120, 144, 300, 600, 1200, 1800, 6000, and 36000; units of dry capacity included 6 and 12; units of liquid capacity 3, 6, 12, 24, and 144; and units of weight include 60, 300, 600, 18000, and 36000. (And remember their hexameter, i.e., verse of six "feet", the oldest and preeminent metre of their poetry.)
* Middle Ages and Olde Measurements:
- The Brits: According to the Encyclopedia of Scientific Units, the Lea (or Lay) was a British unit of length of 360 feet. (By the way, there was quite a bit of technological advancement going on in the Middle Ages.)
- The Scots: Units of length included 6, 12, and 24
- The Irish: Units of length included 3, 6, 12, and 36.
- The French: Units of weight included 3, 12, 24 and 72 (i.e., 360/5; of course the modern metric weights are all factors of 10); units of length included 3, 6, 12, 72, 144, 12,000, and 144,000, units of liquid capacity included 18, 36, 72, and 144.
- The Italians: Units of capacity included 12 and 60; a libbra grossa (big pound) = 12 once (ounces); and a trabucco = 6 piedi (feet).
- The Spaniards: Units of area included 12, 36, 72, and 600 and units of weight included 3, 6, 12, 24, 36, 72, 144, 300, and 2400.
* The Missing Number 7: The division of the week into seven days is ancient. (See rsr.org/7-days-in-a-week.) Yet the number seven, admittedly not factorable, is completely overlooked in ancient weights and measurements. Three and five are not factorable. Yet three appears occasionally being integral to the traditional system. Five appears often as does ten and its multiples because God gave us ten fingers with five per hand for functionality and for learning how to count. So five is a natural unit. A fascinating observation about the number seven for the days in a week is its persistence and ascendancy over alternatives such as the 10-day weeks (three per month) of the Incas, Chinese, and Egyptians. A week of seven days, originating with God's six days of creation and one day of rest, has persisted and now dominates the world even though it is not tied to any astronomical cycle. (It is likely, God being who He is, that a seven-day week is harmonic and reverberates through history in accord with mankind's deep psychophysical meta-circadian rhythm.)
* RSR and Danny Faulkner: We invite you to enjoy these related RSR shows...
- RSR on the 360 Day Year & 360 Day Year Pt. 2 (part 2 of this radio program)
- RSR Report on the Int'l Creation Conference: Bob and Fred Williams commend Danny for rebuking other creationists
- University of South Carolina Astronomer Faulkner on RSR: this show
- RSR: Where's that Blue Star Assembly Line?: The guys discuss Danny's writing about these short-lived stars
- Danny Faulkner on (against) the 360-day Year: this show
- RSR Rebuts Geocentrism: Where Bob references and builds on Faulkner's great geocentrism article
- On the Caution About the 360-Day Year: Enyart's rebuttal in the CRSQ to Faulkner's paper against the 360-day year
And see also:
- Did the Preflood Earth Have a 30-Day Lunar Month by Dr. Robert Brown, Astronautics
- On the origin of the world's first-known number system (a hybrid decimal/base 60 system; see just above)- RSR: 24 Hours in a Day -- An Ancient Measurement
- 360dayyear.com
- rsr.org/3
Request for Help: We would like to list the most ancient references known to a seven day week. If you'd like to do some volunteer research for RSR, please email Bob@rsr.org to let us know and pass along whatever you find. Thanks for your consideration!
Today’s Resource: Have you browsed through our RSR Science Department in the KGOV Store? You just might LOVE IT! We offer a 30-day money back guarantee on all purchases.
* Possible Technical Difficulty: If you have a problem streaming this program, please listen to the download. Of the thousands of our archived programs, this is the only one that inexplicably, intermittently cut out 20 minutes of audio from the middle of the "streamed" audio.